1. 各种排序的原理及java代码实现
java.utils.Arrays这个类中有各种经典的实现,直接对照着学就好了。
1.1 BinarySearch[这个不是sort,但还是放第一了]
二分法查找,前提是数组中元素全部按照顺序(从小到大或者从大到小)排列好了。Android中SparseArray中用到了binarySearch
android.support.v4.util.ContainerHelpers
// This is Arrays.binarySearch(), but doesn't do any argument validation.
static int binarySearch(int[] array, int size, int value) {
int lo = 0;
int hi = size - 1;
while (lo <= hi) {
int mid = (lo + hi) >>> 1;
int midVal = array[mid];
if (midVal < value) {
lo = mid + 1;
} else if (midVal > value) {
hi = mid - 1;
} else {
return mid; // value found
}
}
return ~lo; // value not present()
}
最后一个用的是位非操作,就是把int(4 bytes)转成2进制所有的0变成1,所有的1变成0.
1.2 BubbleSort
把较大的元素挪到右边,较小的元素挪到左边。
每次从左到右边,两个两个的比较,大的往右挪,第一次完成后,最大的一个一定已经挪到最后了。接下里对n-1个元素进行同样的操作。
java代码
public static void bubbleSort(int[] numArray) {
int n = numArray.length;
int temp = 0;
for (int i = 0; i < n; i++) {
for (int j = 1; j < (n - i); j++) {
if (numArray[j - 1] > numArray[j]) {
temp = numArray[j - 1];
numArray[j - 1] = numArray[j];
numArray[j] = temp;
}
}
}
}
Python实现,python中swap两个值非常方便:
a , b = b , a
def bubble_sort(lists):
# 冒泡排序
count = len(lists)
for i in range(0, count):
for j in range(i + 1, count):
if lists[i] > lists[j]:
lists[i], lists[j] = lists[j], lists[i]
return lists
其实任何语言都应该有这种不用第三个值去swap两个int的方法
x = x + y; // x now becomes 15
y = x - y; // y becomes 10
x = x - y; // x becomes 5
the worst case scenario :array完全倒序 o(n^2)
the best case scenario : array已经排序好 Ω(n)
1.3 Insertion Sort
基本上就是把一个数组从左到右迭代,第一遍声明第一个元素是sorted,第二遍看下第二个和第一个是不是有序的,第二遍完成后第二个元素是sorted。第三遍把前三个排序好。
下面这段代码是从华盛顿大学教程抄的,应该没问题。
public static void insertionSort(int[] a){
for (int i=1;i<a.length;i++){
int temp = a[i];
int j;
for(j=i-1;j>=0&&temp<a[j];j--)
a[j+1] = a[j]
a[j+1] = temp;
}
}
核心算法就是第N此排序完成后,前N个元素已经排序完毕。
the worst case scenario :array完全倒序 o(n^2)
the best case scenario : array已经排序好 Ω(n)
1.4 Merge Sort
这个算法比较复杂,一图胜千言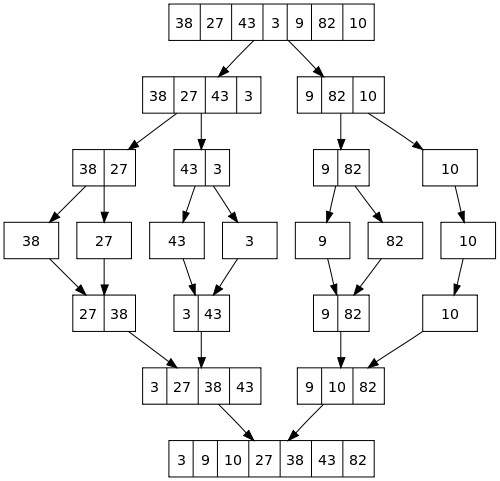
参考
其实就是把array打成一半一半,直到变成多个大小为2的数组,然后再合并起来。java代码直接复制粘贴了,保留包名是对作者的尊重:
package com.java2novice.sorting;
public class MyMergeSort {
private int[] array;
private int[] tempMergArr;
private int length;
public static void main(String a[]){
int[] inputArr = {45,23,11,89,77,98,4,28,65,43};
MyMergeSort mms = new MyMergeSort();
mms.sort(inputArr);
for(int i:inputArr){
System.out.print(i);
System.out.print(" ");
}
}
public void sort(int inputArr[]) {
this.array = inputArr;
this.length = inputArr.length;
this.tempMergArr = new int[length];
doMergeSort(0, length - 1);
}
private void doMergeSort(int lowerIndex, int higherIndex) {
if (lowerIndex < higherIndex) {
int middle = lowerIndex + (higherIndex - lowerIndex) / 2;
// Below step sorts the left side of the array
doMergeSort(lowerIndex, middle);
// Below step sorts the right side of the array
doMergeSort(middle + 1, higherIndex);
// Now merge both sides
mergeParts(lowerIndex, middle, higherIndex);
}
}
private void mergeParts(int lowerIndex, int middle, int higherIndex) {
for (int i = lowerIndex; i <= higherIndex; i++) {
tempMergArr[i] = array[i];
}
int i = lowerIndex;
int j = middle + 1;
int k = lowerIndex;
while (i <= middle && j <= higherIndex) {
if (tempMergArr[i] <= tempMergArr[j]) {
array[k] = tempMergArr[i];
i++;
} else {
array[k] = tempMergArr[j];
j++;
}
k++;
}
while (i <= middle) {
array[k] = tempMergArr[i];
k++;
i++;
}
}
}
1.5 Selection Sort
每次把数组里面最小的元素挪到最左边,图片是从这里抄的
java代码也是抄的
package com.java2novice.algos;
public class MySelectionSort {
public static int[] doSelectionSort(int[] arr){
for (int i = 0; i < arr.length - 1; i++)
{
int index = i;
for (int j = i + 1; j < arr.length; j++)
if (arr[j] < arr[index])
index = j;
int smallerNumber = arr[index];
arr[index] = arr[i];
arr[i] = smallerNumber;
}
return arr;
}
public static void main(String a[]){
int[] arr1 = {10,34,2,56,7,67,88,42};
int[] arr2 = doSelectionSort(arr1);
for(int i:arr2){
System.out.print(i);
System.out.print(", ");
}
}
}
注意,每次遍历都都会意味着数组分为有序和无序两部分,遍历是从无序的数组第一个开始的,并且将无序数组中的最小值与无序数组第一个元素swap一下。
就是很直观的每次把最小的拿到最左边的做法。
1.6 Quicksort
一种比较快速的排序方法
视频
选中数组最后一个元素,称之为pivot。然后从左到右找,把所有小于pivot的元素挪到左边。然后把pivot挪到刚才那个元素右边,一直重复下去。
public static void quickSort(int[] data,int low,int high) {
if (low < high) {
int povit = partition(data, low, high);
quickSort(data, low, povit - 1);
quickSort(data, povit + 1, high);
}
}
public static int partition(int[] arr,int low , int high){
int pivot = arr[low];
while (low < high) {
while (low<high&&arr[high]>=pivot)
{
--high;
}
arr[low] = arr[high];
while (low<high&&arr[low]<=pivot)
{
++low;
}
arr[high] = arr[low];
}
arr[low] = pivot;
return low;
}
这是好不容易看懂的快速排序java实现,感受下手写快排
另一种使用递归的方式
public static void main(String[] args) {
int[] array = {1, 4, 2, 45, 6, 4, 2, 4, 7, 10, 24, 12, 14, 17, 10, 9, 4};
QuickSort(array, 0, array.length-1);
Utils.printEach(array);
}
private static void QuickSort(int[] arr, int start, int end) {
if (start < end) {
int key = arr[start];
int i = start, j;
for (j = start+1;j<=end;j++) {
if (arr[j] < key) {
Utils.swap(arr, j, i + 1);
i++;
}
}
arr[start] = arr[i];
arr[i] = key;
QuickSort(arr, start, i - 1);
QuickSort(arr, i+1, end);
}
}
1.7 TimSort
java的Collections.sort的算法,
Comparison Method Violates Its General Contract!)
2. 二叉树
2.1 二叉查找树(BST)
定义:
在二叉查找树中:
(01) 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
(02) 任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
(03) 任意节点的左、右子树也分别为二叉查找树。
(04) 没有键值相等的节点(no duplicate nodes)。
求BST的最小值
//求BST的最小值
public TreeNode getMin(TreeNode root)
{
if(root==null)
return null;
while(root.left!=null)
root=root.left;
return root;
}
求BST的最大值
//求BST的最大值
public TreeNode getMax(TreeNode root)
{
if(root==null)
return null;
while(root.right!=null)
root=root.right;
return root;
}
查找BST中某节点的前驱节点.即查找数据值小于该结点的最大结点。
public TreeNode preNode(TreeNode x)
{
if(x==null)
return null;
// 如果x存在左孩子,则"x的前驱结点"为 "以其左孩子为根的子树的最大结点"。
if(x.left!=null)
return getMax(x.left);//直接找左树的最大节点就好了,就是一直往左找
// 如果x没有左孩子。则x有以下两种可能:
// (01) x是"一个右孩子",则"x的前驱结点"为 "它的父结点"。
// (02) x是"一个左孩子",则 前驱节点为x的某一个祖先节点的父节点,而且该祖先节点是作为其父节点的右儿子
TreeNode p=x.parent;
while(p!=null&&p.left==x)
{
x=p;//父节点置为新的x
p=p.parent; //父节点的父节点置为新的父节点
}
return p;
}
查找BST中某节点的后继节点.即查找数据值大于该结点的最小结点。
public TreeNode postNode(TreeNode x)
{
if(x==null)
return null;
// 如果x存在右孩子,则"x的后继结点"为 "以其右孩子为根的子树的最小结点"。
if(x.left!=null)
return getMin(x.right);
// 如果x没有右孩子。则x有以下两种可能:
// (01) x是"一个左孩子",则"x的后继结点"为 "它的父结点"。
// (02) x是"一个右孩子",则 前驱节点为x的某一个祖先节点的父节点,而且该祖先节点是作为其父节点的左儿子
TreeNode p=x.parent;
while(p!=null&&p.right==x)
{
x=p;//父节点置为新的x
p=p.parent; //父节点的父节点置为新的父节点
}
return p;
}
给出一个Int值,查找这个Int值在树中对应的节点
//递归
public TreeNode findNode(TreeNode head, int val){
if(head==null){
return null;
}
if(head.val==val){
return head;
}else if(head.val > val){
head = head.left;
}else {
head= head.right;
}
return findNode(head, val);
}
//非递归
public TreeNode findNode(TreeNode head, int val){
if(head==null){
return null;
}
while(head!=null){
if(head.val ==val){
return head;
}else if (head.val > val){
head = head.left;
}else {
head = head.right;
}
}
return head;
}
插入值
//BST插入节点 --递归版--
public TreeNode insertRec(TreeNode root,TreeNode x)
{
if(root==null)
root=x;
else if(x.value<root.value)
root.left=insertRec(root.left, x);
else if(x.value>root.value)
root.right=insertRec(root.right, x);
return root;
}
//BST插入节点 --非 递归版--
public TreeNode insert(TreeNode root,TreeNode x)
{
if(root==null)
root=x;
TreeNode p=null;//需要记录父节点
while(root!=null)//定位插入的位置
{
p=root;//记录父节点
if(x.value<root.value)
root=root.left;
else
root=root.right;
}
x.parent=p;//定位到合适的页节点的空白处后,根据和父节点的大小比较插入合适的位置
if(x.value<p.value)
p.left=x;
else if(x.value>p.value)
p.right=x;
return root;
}
参考
3. 链表
有环链表的判断问题。时间复杂度和空间复杂度的最优解是创建两根迭代速度不一样的指针
下面的代码来自csdn
public class LinkLoop {
public static boolean hasLoop(Node n){
//定义两个指针tmp1,tmp2
Node tmp1 = n;
Node tmp2 = n.next;
while(tmp2!=null){
int d1 = tmp1.val;
int d2 = tmp2.val;
if(d1 == d2)return true;//当两个指针重逢时,说明存在环,否则不存在。
tmp1 = tmp1.next; //每次迭代时,指针1走一步,指针2走两步
tmp2 = tmp2.next.next;
if(tmp2 == null)return false;//不存在环时,退出
}
return true; //如果tmp2为null,说明元素只有一个,也可以说明是存在环
}
//方法2:将每次走过的节点保存到hash表中,如果节点在hash表中,则表示存在环
public static boolean hasLoop2(Node n){
Node temp1 = n;
HashMap<Node,Node> ns = new HashMap<Node,Node>();
while(n!=null){
if(ns.get(temp1)!=null)return true;
else ns.put(temp1, temp1);
temp1 = temp1.next;
if(temp1 == null)return false;
}
return true;
}
public static void main(String[] args) {
Node n1 = new Node(1);
Node n2 = new Node(2);
Node n3 = new Node(3);
Node n4 = new Node(4);
Node n5 = new Node(5);
n1.next = n2;
n2.next = n3;
n3.next = n4;
n4.next = n5;
n5.next = n1; //构造一个带环的链表,去除此句表示不带环
System.out.println(hasLoop(n1));
System.out.println(hasLoop2(n1));
}
}
给定两单链表A、B,只给出两头指针。请问:
1、如何判断两单链表(无环)是否相交?
有两种可取的办法:
(1)人为构环,将链表A的尾节点指向链表B,再判断是否构环成功?从链表B的头指针往下遍历,如果能够回到B,则说明相交
(2)判断两链表最后一个节点是否相同,如果相交,则尾节点肯定是同一节点
2、如何判断两单链表(不知是否有环)相交?
先判断是否有环,判断是否有环可以使用追逐办法,设置两个指针,一个走一步,一个走两步,如果能相遇则说明存在环
(1)两个都没环:回到问题1
(2)一个有环,一个没环:不用判断了,肯定两链表不相交
(3)两个都有环:判断链表A的碰撞点是否出现在链表B的环中,如果在,则相交。(相交时,环必定是两链表共有的)
3.最小栈的实现
需要两个栈,A和B,B用于存储A中当前min的index,B中由上而下依次是A的最小,第二小,第三小。。。所以万一A中的最小被pop掉了,直接拿B顶上的元素,始终是最小的。时间复杂度是O(1),空间复杂度最坏是O(N)
4.在O(1)时间复杂度删除链表节点
class Solution:
# @param node: the node in the list should be deleted
# @return: nothing
def deleteNode(self, node):
temp = node.next
node.val = temp.val
node.next = temp.next
# write your code here
- 堆排序的实现
堆排序,时间复杂度O(nlogn),任何时刻都只需要常数个额外的元素空间存储临时数据。
堆的定义
n个元素的序列{k1,k2,…,kn}当且仅当满足下列关系之一时,称之为堆。
情形1:ki <= k2i 且ki <= k2i+1 (最小化堆或小顶堆)
情形2:ki >= k2i 且ki >= k2i+1 (最大化堆或大顶堆)
其中i=1,2,…,n/2向下取整;
堆可以看成是完全二叉树,完全二叉树中所有非终端结点的值均不大于(或不小于)其左、右孩子结点的值。
排序通常用最大堆,构造优先队列通常用最小堆。最大堆(大顶堆)和最小堆实现基本一样,只要修改维护堆性质的函数即可。
Java实现—堆排序 Heap Sort
堆排序方法对记录数较少的文件并不值得提倡,但对n较大的文件还是很有效的。因为其运行时间主要耗费在建初始堆和调整建新堆时进行的反复“筛选”上。
任意一位置i上元素,其左儿子为2i+1上,右儿子在2i+2上。
我碰到过的算法题(还是面试官手下留情的):
- 两个整形数组,请使用你能够想到的最优算法,实现求交集的操作
- 二维数组环形打印
- 给定一个n*m矩阵,求从左上角到右下角总共存在多少条路径,每次只能向右走或者向下走。
递归和动态规划
首先给出计算总的可能路径的方法
public static int uniquePaths(int m, int n){
if(m==0 || n==0) return 0;
if(m ==1 || n==1) return 1;
int[][] dp = new int[m][n];
//只有一行时,到终点每个格子只有一种走法
for (int i=0; i<n; i++)
dp[0][i] = 1;
// 只有一列时,到终点每个格子只有一种走法
for (int i=0; i<m; i++)
dp[i][0] = 1;
// for each body node, number of path = paths from top + paths from left
for (int i=1; i<m; i++){
for (int j=1; j<n; j++){
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];
}
解法二:数学中的组合问题,因为从左上角到右下角,总共需要走n+m-2步,左上角和右下角的元素不考虑在内,我们每次都可以选择向下走,向下走总共需要m-1步,所以在n+m-2步中选择m-1步,这是典型的排列组合问题。
int uniquePaths(int m, int n)
{
int N = n + m - 2;
int K = n - 1;
double res = 1.0;
for (int i = 1; i <= n - 1; ++i)
{
res = res * (N - K + i) / i;
}
return (int)res;
}
KMP算法
